Big-O Notation
Table of Contents
Concept
In Computer Science, it is fascinating to analyze the cost of an algorithm in the worst case.
Given a large input size, Big O notation is one of the most fundamental tools to measure an algorithm’s cost.
Big-O Notation
Computer scientists are concerned with how a function grows when a huge input is given. So, a small input or constant factors are not considered when analyzing the cost of the function.
Big-O is defined as the asymptotic upper bound of a function.
Let $f(x)$ be the function we want to measure, and $g(x)$ be another function that only contains the dominant term of $f(x)$. Here, $g(x)$ is always less than $f(x)$.
In a formal definition of Big-O,
- $f(x) \in O(g(x))$ if there exists positive constants $c$ and $x_0$ such that $f(x) \leq c*g(x)$ for all $x \geq x_0$.
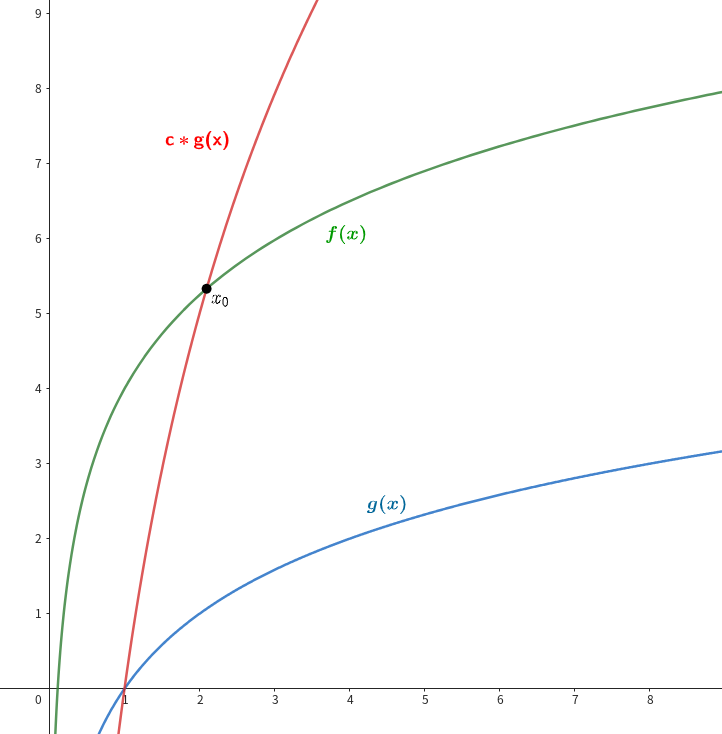
This is pronounced as Order of ~ or Big O of ~.
Big-O Properties
If the function $f$ can be written as a finite sum of other functions, then the fastest growing one determines the order of $f(x)$.
\[f(x) = 4logx + 5(logx)^2 + x^2 + 3x^4 \in O(x^4)\ \ \ \ \ as\ x \rightarrow \infty\]In other words, it disregards coefficient, constant, and lower-order terms of the polynomial.
Note that, $log(x^c) = c*log(x) \rightarrow O(log(x^c)) = O(logx)$.
For multiplication by a constant or a function,
- $f*O(g) = O(f*g)$
- $O(|k|*g) = O(g)$ where $k$ is constant
For multiple functions, when $f_1 \in O(g_1)$ and $f_2 \in O(g_2)$,
- $f_1f_2 \in O(g_1g_2)$
- $f_1 + f_2 \in O(max(g_1, g_2))$
For multiple variables,
- $f(x,y) = 4x^2 + 5y^3 \in O(x^2 + y^3)$
Complexity
An algorithm’s complexity is typically determined by the dominant time-consuming section of the function that implements the algorithm.
For a function that contains many different iterative parts, the greatest iteration happens to dominate its time complexity.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def print_matrix_sum(m: list[list[int]]) -> None:
# Suppose that a square matrix is given.
n = len(m)
""" T(n) -> O(n) """
sum_of_first_col = 0
for i in range(n):
sum_of_first_col += m[i][0]
""" T(n^2 / 2) -> O(n^2) : Ignore coefficient. """
sum_of_triangle = 0
for i in range(n):
for j in range(i+1, n):
sum_of_triangle = m[i][j]
""" T(n * (n^3 / 5)) = T(n^4 / 5) -> O(n^4) : Ignore coefficient. """
sum_of_random = 0
for i in range(n):
j = 0
while j < n**3:
# It is five times as fast to reach the end.
j += 5
# Randomly choose values.
sum_of_random += m[i][j % n]
print("Sum of the first column:", sum_of_first_col)
print("Sum of the right-corner triangle:", sum_of_triangle)
print("Sum of random chosen values:", sum_of_random)
In the above example, function print_matrix_sum takes $O(n^4)$ time
because time complexity calculation ignores coefficient, constant, and smaller terms in the polynomial.
For a recursive function that invokes itself several times, a decision tree that represents subsequent invocations according to function inputs can help us account for time complexity.
If no pruning exists, most recursive functions branching out many times in each invocation will likely take exponential time.
1
2
3
4
5
6
def fibonacci(n: int) -> int:
# Base case: F(1) = F(2) = 1
if n <= 2:
return 1 if n > 0 else 0
# Recursive case: F(n) = F(n-1) + F(n-2)
return fibonacci(n-1) + fibonacci(n-2)
At first glance, it is easy to understand that function fibonacci branches twice in every invocation
until it hits the base case.
Thus, it takes $O(2^n)$ time even though the number of actual computations is less than $2^n$
as shown in the following figure.
fibonacci(5)
/ \
fibonacci(4) fibonacci(3)
/ | | \
fibonacci(3) fibonacci(2) fibonacci(2) fibonacci(1)
/ |
fibonacci(2) fibonacci(1)
In the decision tree, the tree height is the number of consecutive invocations in the worst case, which is the same as the size of call stacks when it reaches the base case. Also, the tree height is usually the input size $n$.
If the function body contains a linear time of iteration, the total time complexity will be $O(n*2^n)$.
For a recursive function that invokes itself exactly once, it is important to guess how the input size will be shrunk. The input range in this type of function is determined by constraints given in each invocation. Some of the given arguments and local variables should be involved.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
""" O(n) """
def factorial(n: int) -> int:
# Base case
if n <= 1:
return 1 if n == 1 else 0
# Recursive case
return n * factorial(n-1)
""" O(log3(n)) """
def ternary_search(arr: list[str], lo: int, hi: int, target: str) -> bool:
# ref: https://en.wikipedia.org/wiki/Ternary_search
# Base case: there is a single element.
if lo >= hi:
return arr[lo] == target
# Divide a given range into three parts.
m1 = lo + (hi - lo) // 3
m2 = hi - (hi - lo) // 3
# Branch out to one of three parts of the current range.
if target < arr[m1]:
# [lo, m1)
return ternary_search(arr, lo, m1-1, target)
if target < arr[m2]:
# [m1, m2)
return ternary_search(arr, m1, m2-1, target)
# [m2, hi]
return ternary_search(arr, m2, hi, target)
See the decision tree of both functions where there is a difference in their depth for the same size of input.
factorial(13) arr = [
| 'Apple', 'Apricot', 'Aratiles', 'Araza', 'Avocado',
factorial(12) 'Banana', 'Bilberry', 'Blackberry', 'Blueberry',
| 'Cherry', 'Coconut', 'Cranberry', 'Currant',
factorial(11) ]
|
factorial(10) ternary_search(arr, 0, 12, "Coconut")
| |
factorial(9) ternary_search(arr, 8, 12, "Coconut")
| |
factorial(8) ternary_search(arr, 9, 10, "Coconut")
| |
factorial(7) ternary_search(arr, 10, 10, "Coconut")
|
factorial(6)
.
.
.
factorial(1)
Two decision trees are all biased in one direction where we can easily find time and space complexity since both complexities are the same as the maximum size of call stacks in the worst case.
Space complexity generally depends on the total memory size of local variables used in a function. The above example assigns two or fewer local variables, which we can ignore in the calculation.
On the other hand, when a function assigns a new container, such as an array or a hash map, we have to consider its size in the space complexity.
Similarly, there are many different methods to mearsure the cost of an algorithm.
| Type | Notation | Description |
|---|---|---|
| Big O | O(n) | the upper bound of the complexity |
| Omega | Ω(n) | the lower bound of the complexity |
| Theta | Θ(n) | the exact bound of the complexity |
| Little O | o(n) | the upper bound excluding the exact bound |
Application
Constant Time
- $O(1)$
- No iteration
1
2
def add(x: int, y: int) -> int:
return x + y
Logarithmic Time
- $O(log_2(n)) \equiv O(log_3(n)) \equiv O(log(n))$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
""" Iterative function """
def binary_search(arr: list[int], target: int) -> bool:
lo, hi = 0, len(arr)
while lo+1 < hi:
mid = (lo + hi) // 2
# Explore the half of the current input size in each iteration.
if arr[mid] < target:
lo = mid
elif arr[mid] > target:
hi = mid
else:
return mid
return -1
""" Recursive function """
def binary_search(arr: list[int], lo: int, hi: int, target: int) -> int:
if lo > hi:
return -1
mid = (lo + hi) // 2
if arr[mid] > target:
return binary_search(arr, lo, mid-1, target)
if arr[mid] < target:
return binary_search(arr, mid+1, hi, target)
return mid
Square Root Time
- $O(\sqrt{n})$
1
2
3
4
5
6
7
8
9
10
11
12
def find_prim_factors(n: int) -> set:
ret = set()
i, x = 2, n
while i*i <= n:
if x % i == 0:
ret.add(i)
x //= i
continue
i += 1
if x > 1:
ret.add(x)
return ret
Linearithmic Time
- $O(n)$
- also known as linear time
1
2
3
4
5
6
7
8
9
10
11
12
13
""" Iterative function """
def sum_array(arr: list[int]) -> int:
# Iterate over elements exactly once.
_sum = 0
for elem in arr:
_sum += elem
return _sum
""" Recursive function """
def calc_factorial(n: int) -> int:
if n == 1:
return n
return n * calc_factorial(n-1)
Squared Time
- $O(n^2)$
- also known as quadratic time
1
2
3
4
5
6
7
8
def add_matrix(m1: list[list], m2: list[list]) -> list[list]:
# Nested loop is required.
n = len(m1)
m3 = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
m3[i][j] = m1[i][j] + m2[i][j]
return m3
Cubed Time
- $O(n^3)$
1
2
3
4
5
6
7
8
9
def multiply_matrix(m1: list[list], m2: list[list]) -> list[list]:
# Something like finding triplets requires 3-nested loops.
n = len(m1)
m3 = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(n):
for k in range(n):
m3[i][j] += m1[i][k] * m2[k][j]
return m3
Linear Logarithmic Time
- $O(n*log(n))$
- There are some of array sorting algorithms.
- For merge sort where it runs in place, it works in two large stages:
- Divide the unsorted list in half until every sublist contains one single element. It takes $O(log(n))$ time.
- In backtracking, repeatedly merge two sub-lists into a new sorted list until the sorted list contains all elements. To sort in merging, it has to iterate over elements exactly once. As shown in the following, it will finally look at all elements $log(n)$ times. That is why it takes $O(n*log(n))$ time.
Base case : (3) (4) (2) (1) (7) (5) (8) (9) (0) (6)
Merge : (3 4) (1 2) (5 7) (8 9) (0 6) -> Iterate n times
Merge : (1 2 3 4) (5 7) (0 6 8 9) -> Iterate n times
Merge : (1 2 3 4 5 7) (0 6 8 9) -> Iterate n times
Merge : (0 1 2 3 4 5 6 7 8 9) -> Iterate n times
n = 10
log2(n) = log2(10) = 3.322
There are 4 depths in a decision tree.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def merge_sort(elems: list, begin: int, end: int) -> None:
# Base case: do not have to sort an array of length 1.
if begin == end:
return
# Recursive case: sort both the left and right half respectively in place.
mid = (begin + end) >> 1
merge_sort(elems, begin, mid)
merge_sort(elems, mid+1, end)
# Merge two sorted parts into one.
temp = [-1] * (end-begin+1)
l, r, i = begin, mid+1, 0
while l <= mid and r <= end:
if elems[l] <= elems[r]:
temp[i] = elems[l]
l += 1
else:
temp[i] = elems[r]
r += 1
i += 1
# Move the rest of the left half part into a temporary array.
while l <= mid:
temp[i] = elems[l]
l += 1
i += 1
# Move the rest of the right half part into a temporary array.
while r <= end:
temp[i] = elems[r]
r += 1
i += 1
# Copy it into the original array.
for i in range(begin, end+1):
elems[i] = temp[i-begin]

Exponential Time
- $O(c^n)$ where $c$ is constant
1
2
3
4
5
6
7
8
""" Exponential Time : O(c^n) """
def recurse(arr: list[int], pos: int, c: int) -> None:
# Base case: it reaches the very end of an array.
if pos == len(arr):
return
# Decision tree with the height of N has c branches in every invocation.
for i in range(pos, pos+c):
recurse(arr, i, c)
Factorial Time
- $O(n!)$
1
2
3
4
5
6
7
8
9
10
11
12
def permutation(arr: list[int], used: int = 0, temp: list[int] = []) -> None:
# Base case: all elements are used.
if used == (1 << len(arr))-1:
print(temp)
return
# Explore the next number by choosing an unused element in this recursion.
for i, elem in enumerate(arr):
if used & (1 << i):
continue
temp.append(elem)
permutation(arr, used | (1 << i), temp)
temp.pop()
For common data structure operations, see here
For python operations, the followings will be helpful.